dmft.twosite

Two Site Dynamical Mean Field Theory

The two site DMFT approach given by M. Potthoff [Potthoff2001] on how to treat the impurity bath as a sigle site of the DMFT. Work is around a single impurity Anderson model.

[Potthoff2001]
  1. Potthoff PRB, 64, 165114, 2001

DMFT solver for an impurity and a single bath site

Functions

dmft.twosite.diagonalize(operator)

diagonalizes single site Spin Hamiltonian

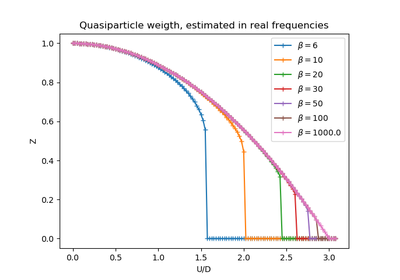
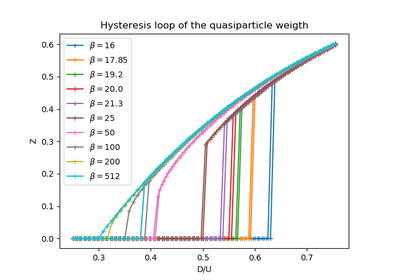
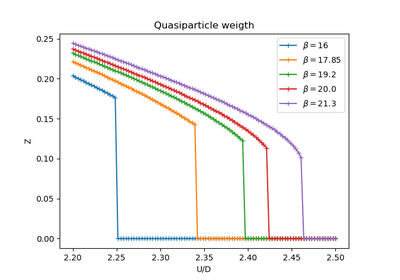
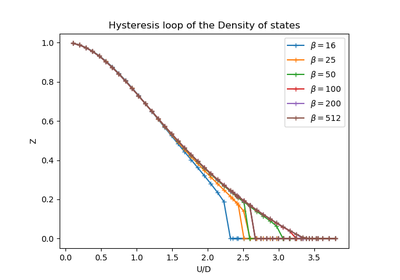
dmft.twosite.dmft_loop(u_int=array([ 0., 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1., 1.05, 1.1, 1.15, 1.2, 1.25, 1.3, 1.35, 1.4, 1.45, 1.5, 1.55, 1.6, 1.65, 1.7, 1.75, 1.8, 1.85, 1.9, 1.95, 2., 2.05, 2.1, 2.15, 2.2, 2.25, 2.3, 2.35, 2.4, 2.45, 2.5, 2.55, 2.6, 2.65, 2.7, 2.75, 2.8, 2.85, 2.9, 2.95, 3., 3.05, 3.1, 3.15]), axis='real', beta=100000.0, hop=0.5, hyb=0.4)

Perform a DMFT loop for the half-filled case of the Two site formulation

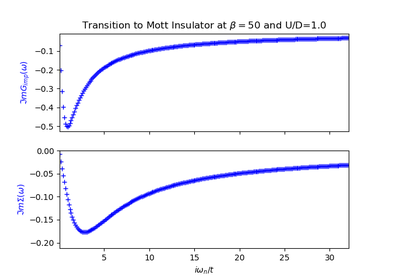
Examples using dmft.twosite.dmft_loop

dmft.twosite.expected_value(operator, eig_values, eig_states, beta)

Calculates the average value of an observable it requires that states and operators have the same base

dmft.twosite.gf_lehmann(eig_e, eig_states, d_dag, beta, omega, d=None, cut=1e-06)

Outputs the lehmann representation of the greens function omega has to be given, as matsubara or real frequencies

dmft.twosite.gw_invfouriertrans(g_iwn, tau, w_n, tail_coef=(1.0, 0.0, 0.0))

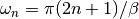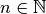Performs an inverse fourier transform of the green Function in which only the imaginary positive matsubara frequencies \omega_n= \pi(2n+1)/\beta with n \in \mathbb{N} are used. The high frequency tails are transformed analytically up to the third moment.

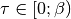Output is the real valued positivite imaginary time green function. For the positive time output \tau \in [0;\beta). Array sizes need not match between frequencies and times, but a time array twice as dense is recommended for best performance of the Fast Fourrier transform.

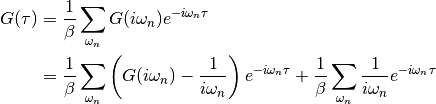
G(\tau) &= \frac{1}{\beta} \sum_{\omega_n} G(i\omega_n)e^{-i\omega_n \tau} \\ &= \frac{1}{\beta} \sum_{\omega_n}\left( G(i\omega_n) -\frac{1}{i\omega_n}\right) e^{-i\omega_n \tau} + \frac{1}{\beta} \sum_{\omega_n}\frac{1}{i\omega_n}e^{-i\omega_n \tau} \\

Parameters:
  • g_iwn (real float array) – Imaginary time interacting Green function
  • tau (real float array) – Imaginary time points
  • w_n (real float array) – fermionic matsubara frequencies. Only use the positive ones
  • tail_coef (list of floats size 3) – The first moments of the tails
Returns:

Interacting Greens function in matsubara frequencies
Return type:

complex ndarray

See also

gt_fouriertrans(), freq_tail_fourier()

dmft.twosite.m2_weight(t)

Calculates the 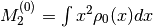M_2^{(0)}=\int x^2 \rho_0(x)dx which is the variance of the non-interacting density of states of a Bethe Lattice

dmft.twosite.matsubara_Z(im_sigma, beta)

Calculates the impurity quasiparticle weight from the imaginary part of the self energy in the matsubara frequencies

Examples using dmft.twosite.matsubara_Z

dmft.twosite.matsubara_freq(beta=16.0, size=256, fer=1)

Calculates an array containing the matsubara frequencies under the formula

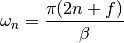
\omega_n = \frac{\pi(2n + f)}{\beta}

where 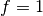f=1 in the case of fermions, and zero for bosons

Parameters:
  • beta (float) – Inverse temperature of the system
  • size (integer) – size of the array : amount of matsubara frequencies
  • fer (0 or 1 integer) – dealing with fermionic particles
Returns:
Return type:

real ndarray
dmft.twosite.quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)

Compute a definite integral.

Integrate func from a to b (possibly infinite interval) using a technique from the Fortran library QUADPACK.

Parameters:
  • func ({function, scipy.LowLevelCallable}) –

    A Python function or method to integrate. If func takes many arguments, it is integrated along the axis corresponding to the first argument.

    If the user desires improved integration performance, then f may be a scipy.LowLevelCallable with one of the signatures:

    double func(double x)
double func(double x, void *user_data)
double func(int n, double *xx)
double func(int n, double *xx, void *user_data)

    The user_data is the data contained in the scipy.LowLevelCallable. In the call forms with xx, n is the length of the xx array which contains xx[0] == x and the rest of the items are numbers contained in the args argument of quad.

    In addition, certain ctypes call signatures are supported for backward compatibility, but those should not be used in new code.

  • a (float) – Lower limit of integration (use -numpy.inf for -infinity).
  • b (float) – Upper limit of integration (use numpy.inf for +infinity).
  • args (tuple, optional) – Extra arguments to pass to func.
  • full_output (int, optional) – Non-zero to return a dictionary of integration information. If non-zero, warning messages are also suppressed and the message is appended to the output tuple.
Returns:

  • y (float) – The integral of func from a to b.
  • abserr (float) – An estimate of the absolute error in the result.
  • infodict (dict) – A dictionary containing additional information. Run scipy.integrate.quad_explain() for more information.
  • message – A convergence message.
  • explain – Appended only with ‘cos’ or ‘sin’ weighting and infinite integration limits, it contains an explanation of the codes in infodict[‘ierlst’]
Other Parameters:
 
  • epsabs (float or int, optional) – Absolute error tolerance.
  • epsrel (float or int, optional) – Relative error tolerance.
  • limit (float or int, optional) – An upper bound on the number of subintervals used in the adaptive algorithm.
  • points ((sequence of floats,ints), optional) – A sequence of break points in the bounded integration interval where local difficulties of the integrand may occur (e.g., singularities, discontinuities). The sequence does not have to be sorted.
  • weight (float or int, optional) – String indicating weighting function. Full explanation for this and the remaining arguments can be found below.
  • wvar (optional) – Variables for use with weighting functions.
  • wopts (optional) – Optional input for reusing Chebyshev moments.
  • maxp1 (float or int, optional) – An upper bound on the number of Chebyshev moments.
  • limlst (int, optional) – Upper bound on the number of cycles (>=3) for use with a sinusoidal weighting and an infinite end-point.

See also

dblquad()
double integral
tplquad()
triple integral
nquad()
n-dimensional integrals (uses quad recursively)
fixed_quad()
fixed-order Gaussian quadrature
quadrature()
adaptive Gaussian quadrature
odeint()
ODE integrator
ode()
ODE integrator
simps()
integrator for sampled data
romb()
integrator for sampled data
scipy.special()
for coefficients and roots of orthogonal polynomials

Notes

Extra information for quad() inputs and outputs

If full_output is non-zero, then the third output argument (infodict) is a dictionary with entries as tabulated below. For infinite limits, the range is transformed to (0,1) and the optional outputs are given with respect to this transformed range. Let M be the input argument limit and let K be infodict[‘last’]. The entries are:

‘neval’
The number of function evaluations.
‘last’
The number, K, of subintervals produced in the subdivision process.
‘alist’
A rank-1 array of length M, the first K elements of which are the left end points of the subintervals in the partition of the integration range.
‘blist’
A rank-1 array of length M, the first K elements of which are the right end points of the subintervals.
‘rlist’
A rank-1 array of length M, the first K elements of which are the integral approximations on the subintervals.
‘elist’
A rank-1 array of length M, the first K elements of which are the moduli of the absolute error estimates on the subintervals.
‘iord’
A rank-1 integer array of length M, the first L elements of which are pointers to the error estimates over the subintervals with L=K if K<=M/2+2 or L=M+1-K otherwise. Let I be the sequence infodict['iord'] and let E be the sequence infodict['elist']. Then E[I[1]], ..., E[I[L]] forms a decreasing sequence.

If the input argument points is provided (i.e. it is not None), the following additional outputs are placed in the output dictionary. Assume the points sequence is of length P.

‘pts’
A rank-1 array of length P+2 containing the integration limits and the break points of the intervals in ascending order. This is an array giving the subintervals over which integration will occur.
‘level’
A rank-1 integer array of length M (=limit), containing the subdivision levels of the subintervals, i.e., if (aa,bb) is a subinterval of (pts[1], pts[2]) where pts[0] and pts[2] are adjacent elements of infodict['pts'], then (aa,bb) has level l if |bb-aa| = |pts[2]-pts[1]| * 2**(-l).
‘ndin’
A rank-1 integer array of length P+2. After the first integration over the intervals (pts[1], pts[2]), the error estimates over some of the intervals may have been increased artificially in order to put their subdivision forward. This array has ones in slots corresponding to the subintervals for which this happens.

Weighting the integrand

The input variables, weight and wvar, are used to weight the integrand by a select list of functions. Different integration methods are used to compute the integral with these weighting functions. The possible values of weight and the corresponding weighting functions are.

weight Weight function used wvar
‘cos’ cos(w*x) wvar = w
‘sin’ sin(w*x) wvar = w
‘alg’ g(x) = ((x-a)**alpha)*((b-x)**beta) wvar = (alpha, beta)
‘alg-loga’ g(x)*log(x-a) wvar = (alpha, beta)
‘alg-logb’ g(x)*log(b-x) wvar = (alpha, beta)
‘alg-log’ g(x)*log(x-a)*log(b-x) wvar = (alpha, beta)
‘cauchy’ 1/(x-c) wvar = c

wvar holds the parameter w, (alpha, beta), or c depending on the weight selected. In these expressions, a and b are the integration limits.

For the ‘cos’ and ‘sin’ weighting, additional inputs and outputs are available.

For finite integration limits, the integration is performed using a Clenshaw-Curtis method which uses Chebyshev moments. For repeated calculations, these moments are saved in the output dictionary:

‘momcom’
The maximum level of Chebyshev moments that have been computed, i.e., if M_c is infodict['momcom'] then the moments have been computed for intervals of length |b-a| * 2**(-l), l=0,1,...,M_c.
‘nnlog’
A rank-1 integer array of length M(=limit), containing the subdivision levels of the subintervals, i.e., an element of this array is equal to l if the corresponding subinterval is |b-a|* 2**(-l).
‘chebmo’
A rank-2 array of shape (25, maxp1) containing the computed Chebyshev moments. These can be passed on to an integration over the same interval by passing this array as the second element of the sequence wopts and passing infodict[‘momcom’] as the first element.

If one of the integration limits is infinite, then a Fourier integral is computed (assuming w neq 0). If full_output is 1 and a numerical error is encountered, besides the error message attached to the output tuple, a dictionary is also appended to the output tuple which translates the error codes in the array info['ierlst'] to English messages. The output information dictionary contains the following entries instead of ‘last’, ‘alist’, ‘blist’, ‘rlist’, and ‘elist’:

‘lst’
The number of subintervals needed for the integration (call it K_f).
‘rslst’
A rank-1 array of length M_f=limlst, whose first K_f elements contain the integral contribution over the interval (a+(k-1)c, a+kc) where c = (2*floor(|w|) + 1) * pi / |w| and k=1,2,...,K_f.
‘erlst’
A rank-1 array of length M_f containing the error estimate corresponding to the interval in the same position in infodict['rslist'].
‘ierlst’
A rank-1 integer array of length M_f containing an error flag corresponding to the interval in the same position in infodict['rslist']. See the explanation dictionary (last entry in the output tuple) for the meaning of the codes.

Examples

Calculate 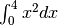\int^4_0 x^2 dx and compare with an analytic result

>>> from scipy import integrate
>>> x2 = lambda x: x**2
>>> integrate.quad(x2, 0, 4)
(21.333333333333332, 2.3684757858670003e-13)
>>> print(4**3 / 3.)  # analytical result
21.3333333333

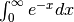
Calculate \int^\infty_0 e^{-x} dx

>>> invexp = lambda x: np.exp(-x)
>>> integrate.quad(invexp, 0, np.inf)
(1.0, 5.842605999138044e-11)

>>> f = lambda x,a : a*x
>>> y, err = integrate.quad(f, 0, 1, args=(1,))
>>> y
0.5
>>> y, err = integrate.quad(f, 0, 1, args=(3,))
>>> y
1.5

Calculate 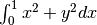\int^1_0 x^2 + y^2 dx with ctypes, holding y parameter as 1:

testlib.c =>
    double func(int n, double args[n]){
        return args[0]*args[0] + args[1]*args[1];}
compile to library testlib.*

from scipy import integrate
import ctypes
lib = ctypes.CDLL('/home/.../testlib.*') #use absolute path
lib.func.restype = ctypes.c_double
lib.func.argtypes = (ctypes.c_int,ctypes.c_double)
integrate.quad(lib.func,0,1,(1))
#(1.3333333333333333, 1.4802973661668752e-14)
print((1.0**3/3.0 + 1.0) - (0.0**3/3.0 + 0.0)) #Analytic result
# 1.3333333333333333
dmft.twosite.refine_mat_solution(end_solver, u_int)

Takes the end converged dmft solver in matsubara frequencies and increases the range of the matsubara frequencies to get nicer plots

Examples using dmft.twosite.refine_mat_solution

Classes

class dmft.twosite.TwoSite(beta, t)

Base class for a two site DMFT solver Sets up environment

Parameters:
  • beta (float) – Inverse temperature of the system
  • t (float) – Hopping amplitude between first neighbor lattice sites
  • freq_axis (string) – ‘real’ or ‘matsubara’ frequencies
GF

dictionary – Stores the Green functions and self energy

double_ocupation()

Calculates the double ocupation of the impurity

expected(observable)

Wrapper to the expected_value function to fix the eigenbasis

hamiltonian()

Two site single impurity anderson model generate the matrix operators that will be used for this hamiltonian

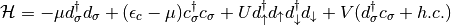
\mathcal{H} = -\mu d^\dagger_\sigma d_\sigma + (\epsilon_c - \mu) c^\dagger_\sigma c_\sigma + U d^\dagger_\uparrow d_\uparrow d^\dagger_\downarrow d_\downarrow + V(d^\dagger_\sigma c_\sigma + h.c.)

hyb_V()

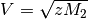
Returns the hybridization parameter V=\sqrt{zM_2}

imp_free_gf(e_c, hyb)

Outputs the Green’s Function of the free propagator of the impurity

ocupations(top=2)

gets the ocupation of the impurity

solve(e_c, u_int, hyb)

Solves the impurity problem

update_H(e_c, u_int, hyb)

Updates impurity hamiltonian and diagonalizes it

class dmft.twosite.TwoSite_Matsubara(beta=100, t=1, nfreq=20)

DMFT solver on the matsubara frequency axis

class dmft.twosite.TwoSite_Real(beta=100000.0, t=1, omega=array([-6., -5.98999166, -5.97998332, ..., 5.97998332, 5.98999166, 6. ]))

DMFT solver in the real axis

imp_z()

Calculates the impurity quasiparticle weight from the real part of the self energy