IPT Hysteresis loop

Within the iterative perturbative theory (IPT) the aim is to find the coexistance regions.

from __future__ import division, absolute_import, print_function

from dmft.ipt_imag import dmft_loop
from dmft.common import greenF, tau_wn_setup, fit_gf
from dmft.twosite import matsubara_Z

import numpy as np
import matplotlib.pylab as plt


def hysteresis(beta, u_range):
    log_g_sig = []
    tau, w_n = tau_wn_setup(dict(BETA=beta, N_MATSUBARA=beta))
    g_iwn = greenF(w_n)
    for u_int in u_range:
        g_iwn, sigma = dmft_loop(u_int, 0.5, g_iwn, w_n, tau)
        log_g_sig.append((g_iwn, sigma))
    return log_g_sig


U = np.linspace(0.1, 3.8, 41)
U = np.concatenate((U, np.linspace(3.6, 2.4, 16)-0.05))
results = []
betarange = [16, 25, 50, 100, 200, 512]
for beta in betarange:
    results.append(hysteresis(beta, U))

Quasiparticle weight

figz, axz = plt.subplots()
for beta, result in zip(betarange, results):
    u_zet = [matsubara_Z(sigma.imag, beta) for _, sigma in result]
    axz.plot(U, u_zet, '+-', label='$\\beta={}$'.format(beta))
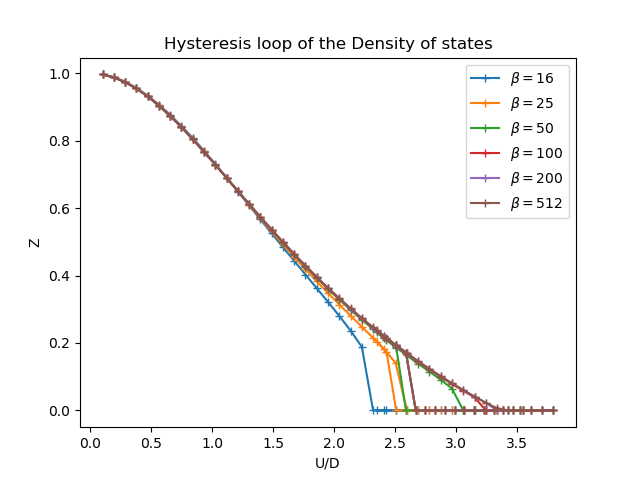
    axz.set_title('Hysteresis loop of the quasiparticle weigth')
    axz.legend(loc=0)
    axz.set_ylabel('Z')
    axz.set_xlabel('U/D')
    axz.set_title('Hysteresis loop of the Density of states')
../../_images/sphx_glr_plot_ipt_coex_001.png

Spectral density at Fermi level

figf, axf = plt.subplots()
for beta, result in zip(betarange, results):
    tau, w_n = tau_wn_setup(dict(BETA=beta, N_MATSUBARA=3))
    u_fl = [-fit_gf(w_n, g_iwn.imag)(0.)for g_iwn, _ in result]
    axf.plot(U, u_fl, 'x:', label='$\\beta={}$'.format(beta))

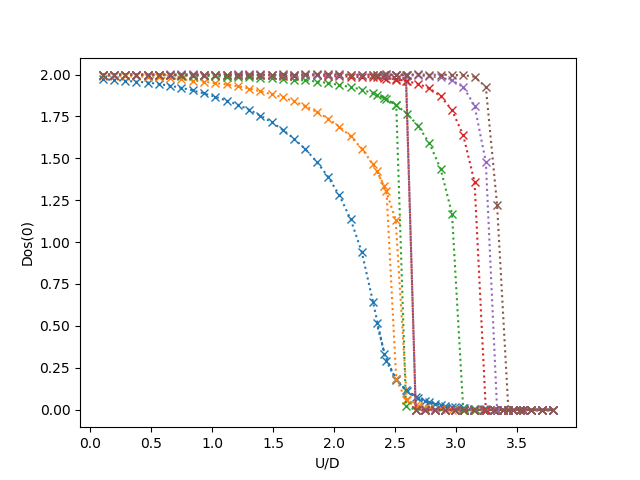
axf.set_ylabel('Dos(0)')
axf.set_xlabel('U/D')
../../_images/sphx_glr_plot_ipt_coex_002.png

Double occupation

Is proportional to the Potential energy by the relation

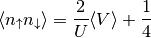
\langle n_\uparrow n_\downarrow \rangle = \frac{2}{U}\langle V \rangle+\frac{1}{4}

taking the expression from Potential energy

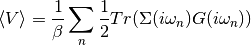
\langle V \rangle = \frac{1}{\beta} \sum_{n} \frac{1}{2} Tr(\Sigma(i\omega_n)G(i\omega_n))

Which tail behaves as

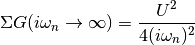
\Sigma G(i\omega_n\rightarrow \infty) = \frac{U^2}{4(i\omega_n)^2}

Upon which one can perform the sum including the tail analytically. The trace for the single band does not influence in this case. The required numerical expression becomes:

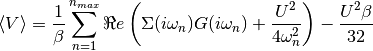
\langle V \rangle = \frac{1}{\beta} \sum_{n=1}^{n_{max}}\Re e \left( \Sigma(i\omega_n)G(i\omega_n) + \frac{U^2}{4\omega_n^2} \right)-\frac{U^2\beta}{32}

figd, axd = plt.subplots()
for beta, result in zip(betarange, results):
    tau, w_n = tau_wn_setup(dict(BETA=beta, N_MATSUBARA=beta))
    V = np.asarray([(s*g+u**2/4./w_n**2).real.sum()/beta
                    for (g, s), u in zip(result, U)]) - beta*U**2/32.

    D = 2./U*V + 0.25
    axd.plot(U, D, '-', label='$\\beta={}$'.format(beta))

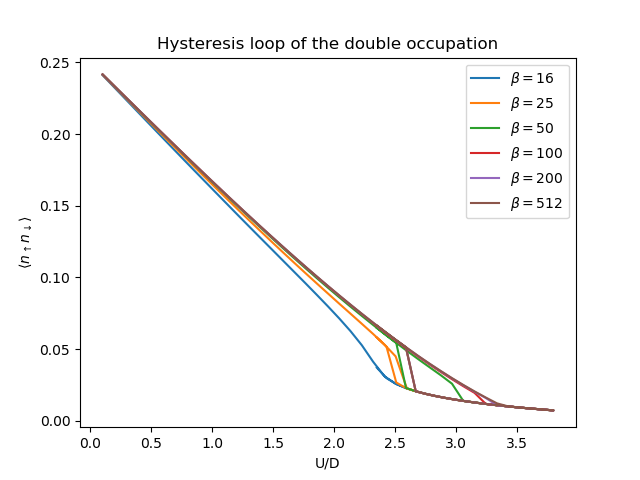
axd.set_title('Hysteresis loop of the double occupation')
axd.legend(loc=0)
axd.set_ylabel(r'$\langle n_\uparrow n_\downarrow \rangle$')
axd.set_xlabel('U/D')
../../_images/sphx_glr_plot_ipt_coex_003.png

Total running time of the script: ( 0 minutes 2.451 seconds)

Download Python source code: plot_ipt_coex.py
Download Jupyter notebook: plot_ipt_coex.ipynb

Generated by Sphinx-Gallery