Transition on free energy

Using the formalism presented in [1] I calculate the stability of the IPT solution within the coexistence region.

[1]	Moeller, G., V. Dobrosavljevi’c, & Ruckenstein, A. E. (1999). RKKY interactions and the Mott transition. Physical Review B, 59(10), 6846–6854. http://dx.doi.org/10.1103/physrevb.59.6846

# Created Fri Apr 21 15:11:05 2017
# Author: Óscar Nájera

from __future__ import division, absolute_import, print_function
import numpy as np
from scipy.integrate import trapz
import matplotlib.pylab as plt

from dmft.ipt_imag import dmft_loop, single_band_ipt_solver
from dmft.common import greenF, tau_wn_setup


def mix(gmet, gins, l):
    return (1 - l) * gins + l * gmet


def one_loop(giw, t, u_int, w_n, tau):
    iw_n = 1j * w_n
    g_0_iwn = 1. / (iw_n - t**2 * giw)
    g_iwn, sigma_iwn = single_band_ipt_solver(u_int, g_0_iwn, w_n, tau)
    return g_iwn


def free_energy_change(beta, u_int, mix_grid):

    tau, w_n = tau_wn_setup(dict(BETA=beta, N_MATSUBARA=2**11))

    ig_iwn, is_iwn = dmft_loop(
        u_int, 0.5, -1.j / (w_n - 1 / w_n), w_n, tau, conv=1e-10)

    mg_iwn, ms_iwn = dmft_loop(u_int, 0.5, greenF(w_n), w_n, tau, conv=1e-10)

    solution_diff = mg_iwn - ig_iwn

    integrand = []
    for l in mix_grid:
        g_in = mix(mg_iwn, ig_iwn, l)
        g_grad = one_loop(g_in, 0.5, U, w_n, tau) - g_in
        integrand.append(np.dot(g_grad, solution_diff).real / beta)

    return np.array([0] + [trapz(integrand[:i], mix_grid[:i])
                           for i in range(2, len(mix_grid) + 1)])


mix_grid = np.linspace(0, 1, 201)

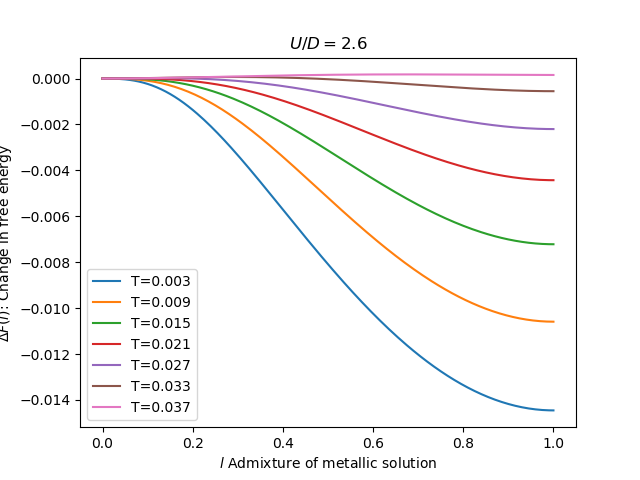
High in the coexistence region

U = 2.6
for temp in [0.003, 0.009, 0.015, 0.021, 0.027, 0.033, 0.037]:
    beta = 1 / temp
    delta_f = free_energy_change(beta, U, mix_grid)
    plt.plot(mix_grid, delta_f, label='T={:.3}'.format(1 / beta))
plt.xlabel('$l$ Admixture of metallic solution')
plt.ylabel(r'$\Delta F(l)$: Change in free energy')
plt.title('$U/D={}$'.format(U))
plt.legend(loc=0)
plt.show()

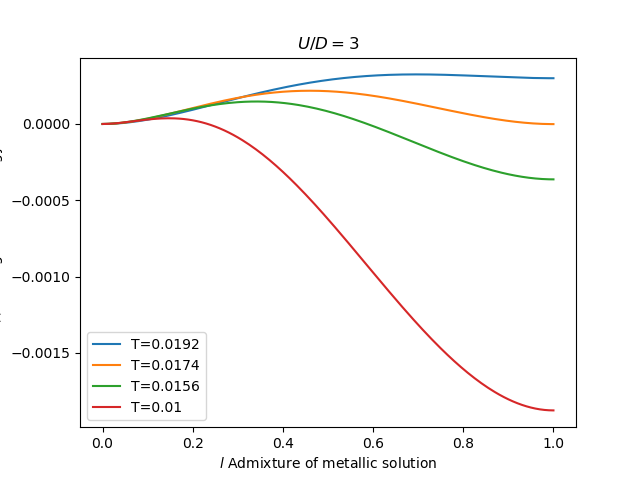
Lower in the coexistence region

U = 3
for beta in [52., 57.38, 64., 100.]:
    delta_f = free_energy_change(beta, U, mix_grid)
    plt.plot(mix_grid, delta_f, label='T={:.3}'.format(1 / beta))
plt.xlabel('$l$ Admixture of metallic solution')
plt.ylabel(r'$\Delta F(l)$: Change in free energy')
plt.title('$U/D={}$'.format(U))
plt.legend(loc=0)

Total running time of the script: ( 0 minutes 9.189 seconds)