Energy formulas¶
Kinetic Energy¶
This energy is the weigthed average of non-interacting kinetic energy. Assuming a non-interacting Hamiltonian in momentum space the kinetic average is.
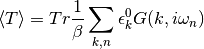
It can be transformed into a treatable form relying on local quantities
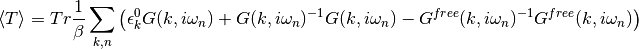
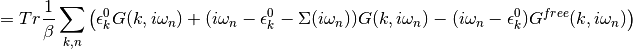
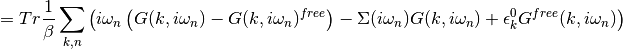
The first two terms can be summed in reciprocal space to yield a local the quantities that come out of the DMFT self-consistency and the last term as it belongs to the non-interacting system is trivially solvable
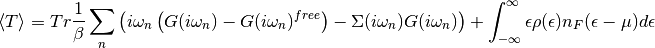
It is also possible to take a simpler approac by introducing a zero to the frequecy sum, with a constant factor. In this case one takes from
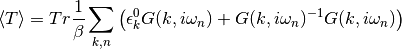
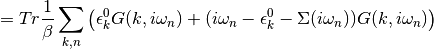
But the local self-energy can be expresed by
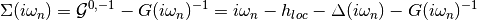
Where 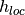 is the momentum independent part of the
hamiltonian. Then the expression transforms into.
is the momentum independent part of the
hamiltonian. Then the expression transforms into.
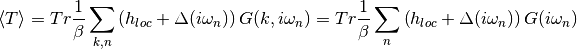
Potential energy¶
According to [Fetter-Walecka] in equation 23.14 then transformed to Matsubara frequencies the potential energy can be described by:
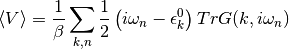
And expressing it in local quantities with the DMFT approximation that the Self-Energy is local
(1)¶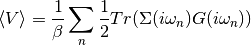
References¶
| [Fetter-Walecka] | Fetter, Walecka, Quantum Theory of many-particle systems |