Thermodynamics of the metallic Dimer lattice

Close to the coexistence region the Energy of the system is calculated.

from math import log, ceil
import numpy as np
from scipy.integrate import simps
import matplotlib.pyplot as plt
import dmft.dimer as dimer
import dmft.common as gf
from dmft.utils import differential_weight

def loop_beta(u_int, tp, betarange, seed):
    avgH = []
    for beta in betarange:
        tau, w_n = gf.tau_wn_setup(
            dict(BETA=beta, N_MATSUBARA=max(2**ceil(log(8 * beta) / log(2)), 256)))
        giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
        if seed == 'I':
            giw_d, giw_o = 1 / (1j * w_n - 4j / w_n), np.zeros_like(w_n) + 0j

        giw_d, giw_o, _ = dimer.ipt_dmft_loop(
            beta, u_int, tp, giw_d, giw_o, tau, w_n, 1e-6)

        ekin = dimer.ekin(giw_d[:int(8 * beta)], giw_o[:int(8 * beta)],
                          w_n[:int(8 * beta)], tp, beta)

        epot = dimer.epot(giw_d[:int(8 * beta)], w_n[:int(8 * beta)],
                          beta, u_int ** 2 / 4 + tp**2 + 0.25, ekin, u_int)
        avgH.append(ekin + epot)

    return np.array(avgH)

fac = np.arctan(25 * np.sqrt(3) / 0.4)
temp = np.tan(np.linspace(5e-3, fac, 195)) * 0.4 / np.sqrt(3)
BETARANGE = 1 / temp

U_int = [1.5, 1.8, 2., 2.5, 2.8, 2.9]
TP = 0.3
avgH = [loop_beta(u_int, TP, BETARANGE, 'M') for u_int in U_int]

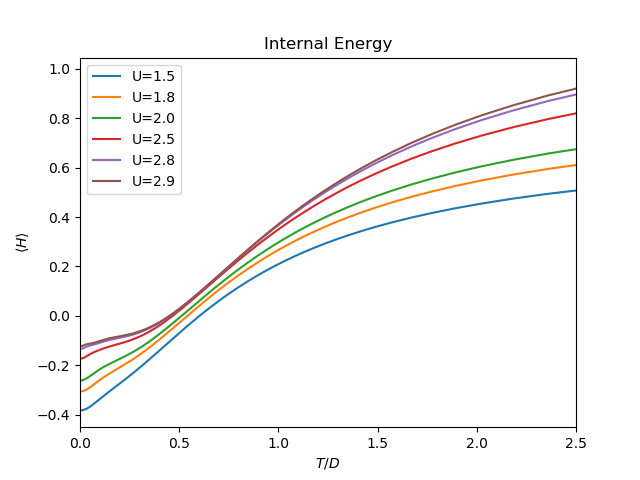
Internal Energy

plt.figure()
temp_cut = sum(temp < 3)
for u, sol in zip(U_int, avgH):
    plt.plot(temp[:temp_cut], sol[:temp_cut], label='U={}'.format(u))

plt.xlim(0, 2.5)
plt.title('Internal Energy')
plt.xlabel('$T/D$')
plt.ylabel(r'$\langle  H \rangle$')
plt.legend(loc=0)

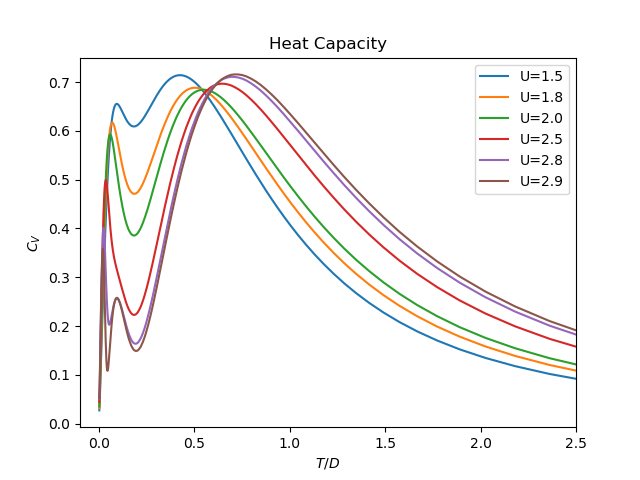
Specific Heat

The Specific heat behaves as expected from a metal being linear close to zero temperature

plt.figure()
CV = [differential_weight(H) / differential_weight(temp) for H in avgH]
for u, cv in zip(U_int, CV):
    plt.plot(temp[:temp_cut], cv[:temp_cut], label='U={}'.format(u))

plt.xlim(-0.1, 2.5)
plt.title('Internal Energy')
plt.title('Heat Capacity')
plt.xlabel('$T/D$')
plt.ylabel(r'$C_V$')
plt.legend(loc=0)

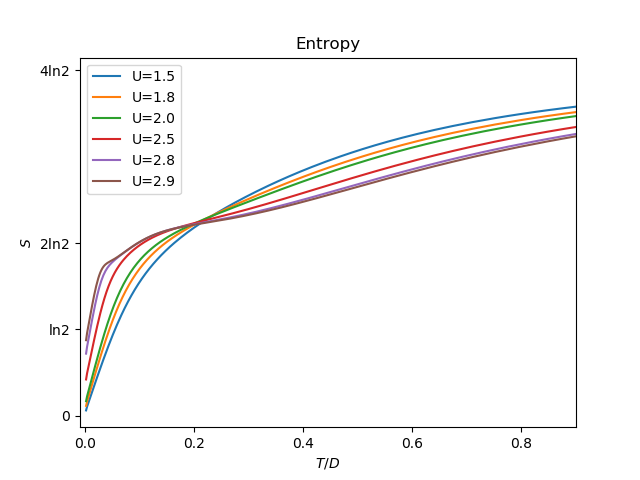
Entropy

Entropy would seem to try to reach a zero value at zero temperature but it does not achieve this goal for all values of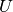

ENDS = []
for cv in CV:
    cv_temp = np.clip(cv, 0, 1) / temp
    s_t = np.array([simps(cv_temp[i:], temp[i:], even='last')
                    for i in range(len(temp))])
    ENDS.append(log(16.) - s_t)

plt.figure()
for u, s in zip(U_int, ENDS):
    plt.plot(temp[:temp_cut], s[:temp_cut], label='U={}'.format(u))

plt.title('Entropy')
plt.xlabel('$T/D$')
plt.ylabel(r'$S$')
plt.legend(loc=0)

plt.xlim(-0.01, 0.9)
plt.yticks([0, log(2), log(2) * 2, log(2) * 4],
           [0, r'$\ln 2$', r'$2\ln 2$', r'$4\ln 2$'])

plt.show()

Total running time of the script: ( 2 minutes 11.753 seconds)