Study the behavior of the Dimer Bethe lattice in the Transition¶
Specific Regions of the phase diagram are reviewed to inspect the behavior of the insulating state
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import dmft.dimer as dimer
import dmft.common as gf
import dmft.ipt_imag as ipt
def loop_u_tp(Drange, tprange, beta, seed='mott gap'):
tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=256))
giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
if seed == 'mott gap':
giw_d, giw_o = 1 / (1j * w_n + 4j / w_n), np.zeros_like(w_n) + 0j
giw_s = []
sigma_iw = []
ekin, epot = [], []
iterations = []
for D, tp in zip(Drange, tprange):
giw_d, giw_o, loops = dimer.ipt_dmft_loop(
beta, 1, tp, giw_d, giw_o, tau, w_n, t=D / 2)
giw_s.append((giw_d, giw_o))
iterations.append(loops)
g0iw_d, g0iw_o = dimer.self_consistency(
1j * w_n, 1j * giw_d.imag, giw_o.real, 0., tp, D**2 / 4)
siw_d, siw_o = ipt.dimer_sigma(1, tp, g0iw_d, g0iw_o, tau, w_n)
sigma_iw.append((siw_d.copy(), siw_o.copy()))
ekin.append(dimer.ekin(giw_d, giw_o, w_n, tp, beta))
epot.append(dimer.epot(giw_d, w_n, beta, 1 / 4 + tp**2, ekin[-1], 1))
print(np.array(iterations))
# last division in energies because I want per spin epot
return np.array(giw_s), np.array(sigma_iw), np.array(ekin) / 4, np.array(epot) / 4, w_n
Drange = np.linspace(0.05, .85, 61)
Drange = np.concatenate((Drange[::-1], Drange))
data = []
for beta in [16., 18., 20., 22., 24., 26., 28., 40., 100., 200.]:
giw_s, sigma_iw, ekin, epot, w_n = loop_u_tp(
Drange, .3 * np.ones_like(Drange), beta, 'met')
data.append((giw_s, sigma_iw, ekin, epot, w_n, beta))
for sim in data:
giw_s, sigma_iw, ekin, epot, w_n, beta = sim
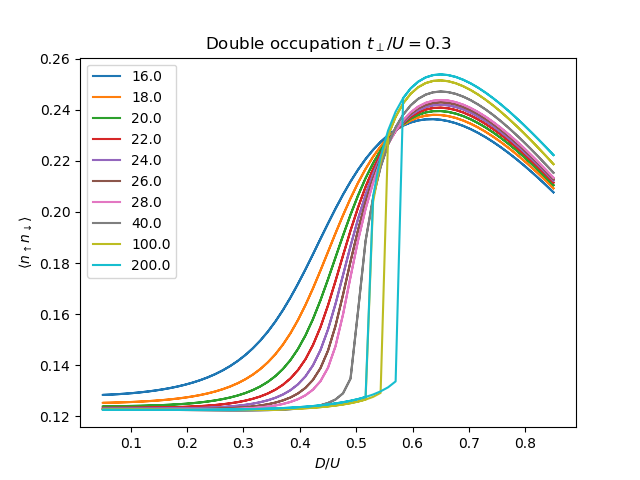
plt.plot(Drange, 2 * epot, '-', label=beta)
plt.title(r'Double occupation $t_\perp/U=0.3$')
plt.ylabel(r'$\langle n_\uparrow n_\downarrow \rangle$')
plt.xlabel(r'$D/U$')
plt.legend()
Out:
[25 21 20 20 19 19 18 18 17 17 17 16 15 14 14 14 13 13 13 12 12 11 11 10 10
9 8 8 7 7 8 9 10 10 10 11 11 10 10 10 10 9 9 9 8 8 7 7 7 7
6 6 6 5 5 5 5 4 4 4 4 1 4 4 4 5 5 5 5 6 6 6 6 7 7
7 8 8 8 9 9 10 10 10 10 11 11 10 10 10 9 8 8 7 8 8 9 10 10 11
11 12 12 13 13 13 14 14 15 16 16 17 17 17 18 18 19 19 20 20 21 21]
[29 23 23 22 22 21 21 20 19 18 18 17 17 17 16 16 15 15 14 13 13 12 11 11 10
9 8 8 8 10 11 12 12 13 13 13 12 12 11 11 10 10 9 9 8 8 7 7 7 6
6 6 6 5 5 5 5 4 4 4 4 1 4 4 4 5 5 5 5 6 6 6 6 7 7
7 8 8 9 9 10 10 11 11 12 12 13 13 13 13 12 11 10 9 8 8 9 10 11 11
12 13 13 14 15 15 16 16 17 17 17 18 18 19 20 21 21 22 22 23 23 24]
[32 26 25 25 24 23 22 22 21 21 20 20 19 19 18 17 17 16 15 15 14 12 12 11 10
10 9 9 11 13 14 15 15 15 15 14 13 12 12 11 10 10 9 9 8 8 7 7 7 6
6 6 5 5 5 5 5 4 4 4 4 1 4 4 4 5 5 5 5 5 6 6 6 7 7
7 8 8 9 9 10 10 11 12 12 13 14 15 15 15 15 14 13 11 9 9 9 10 11 12
12 14 15 15 16 17 17 18 19 19 20 20 21 21 22 22 23 24 25 25 26 27]
[35 28 28 27 26 26 25 25 24 23 22 22 21 20 20 19 18 17 16 16 15 14 13 12 11
10 9 11 14 16 18 18 18 17 16 15 13 12 12 11 10 9 9 8 8 7 7 7 6 6
6 6 5 5 5 5 4 4 4 4 4 1 4 4 4 4 5 5 5 5 6 6 6 6 7
7 7 8 8 9 9 10 11 11 12 13 14 16 17 18 18 18 16 14 12 9 10 11 12 13
14 15 16 16 17 17 19 20 20 21 22 22 23 24 25 25 26 26 27 28 28 29]
[38 31 31 30 29 28 27 27 26 25 25 24 22 22 21 20 20 19 18 17 16 15 14 13 11
10 10 14 18 20 22 21 20 18 16 14 13 12 11 10 10 9 9 8 8 7 7 7 6 6
6 6 5 5 5 5 4 4 4 4 4 1 4 4 4 4 5 5 5 5 5 6 6 6 7
7 7 8 8 8 9 10 10 11 12 13 14 16 18 19 21 22 21 18 15 11 10 11 13 14
15 16 17 18 19 20 20 21 22 22 24 25 25 26 27 27 28 29 30 31 31 32]
[42 34 33 32 32 31 30 28 28 27 26 26 25 24 23 22 21 20 19 18 17 16 15 13 12
10 12 17 22 25 25 23 20 17 15 14 13 12 11 10 9 9 8 8 7 7 7 6 6 6
6 5 5 5 5 5 4 4 4 4 4 1 4 4 4 4 5 5 5 5 5 6 6 6 6
7 7 7 8 8 9 9 10 11 11 12 14 15 17 20 22 25 25 23 18 13 9 12 13 15
16 17 18 19 21 22 22 23 24 25 26 26 27 28 29 30 31 32 32 33 34 35]
[46 37 36 34 34 33 32 31 31 30 29 28 27 26 25 24 23 22 20 19 18 17 16 14 12
10 15 22 28 30 27 23 19 17 15 13 12 11 10 10 9 8 8 8 7 7 7 6 6 6
6 5 5 5 5 4 4 4 4 4 3 1 4 4 4 4 4 5 5 5 5 6 6 6 6
7 7 7 8 8 8 9 9 10 11 12 13 15 16 19 22 26 30 29 23 16 9 12 14 16
17 18 19 20 22 23 24 25 26 27 28 29 30 31 31 32 33 34 34 36 37 38]
[67 54 53 52 50 49 48 47 45 44 43 41 39 38 37 35 34 32 30 29 26 25 22 19 15
19 66 60 32 23 18 16 14 12 11 10 10 9 9 8 8 8 7 7 7 6 6 6 6 5
5 5 5 5 5 4 4 4 4 4 3 1 4 4 4 4 4 4 5 5 5 5 5 6 6
6 6 7 7 7 7 8 8 9 9 10 10 11 12 14 15 18 22 30 54 74 22 15 19 22
25 26 29 30 32 34 35 37 38 39 41 43 44 45 47 48 49 51 52 53 55 56]
[178 145 142 139 136 133 130 127 123 120 115 112 109 105 102 98 93 88
83 78 73 67 59 50 35 33 16 14 13 12 11 10 10 9 9 9
8 8 8 7 7 7 7 6 6 6 6 6 5 5 5 5 5 5
4 4 4 4 4 4 3 1 4 4 4 4 4 4 5 5 5 5
5 5 6 6 6 6 6 7 7 7 7 8 8 8 9 9 9 10
10 11 12 13 14 15 18 22 32 89 68 74 78 84 88 93 98 102
105 110 112 117 120 123 127 130 133 136 139 142 145 148]
[366 301 295 290 282 274 271 263 258 250 243 236 229 222 212 206 197 187
178 166 152 136 121 97 67 27 14 13 12 11 11 10 10 9 9 9
8 8 8 7 7 7 7 7 6 6 6 6 6 5 5 5 5 5
4 4 4 4 4 4 3 1 4 4 4 4 4 4 5 5 5 5
5 6 6 6 6 6 6 7 7 7 7 8 8 8 8 9 9 10
10 11 11 12 13 13 15 16 19 23 37 186 166 179 188 197 206 212
222 231 238 243 250 258 263 271 274 282 290 295 301 307]
data = []
for beta in [16., 18., 20., 22., 24., 26., 28., 40., 100., 200.]:
giw_s, sigma_iw, ekin, epot, w_n = loop_u_tp(
Drange, .15 * np.ones_like(Drange), beta, 'met')
data.append((giw_s, sigma_iw, ekin, epot, w_n, beta))
for sim in data:
giw_s, sigma_iw, ekin, epot, w_n, beta = sim
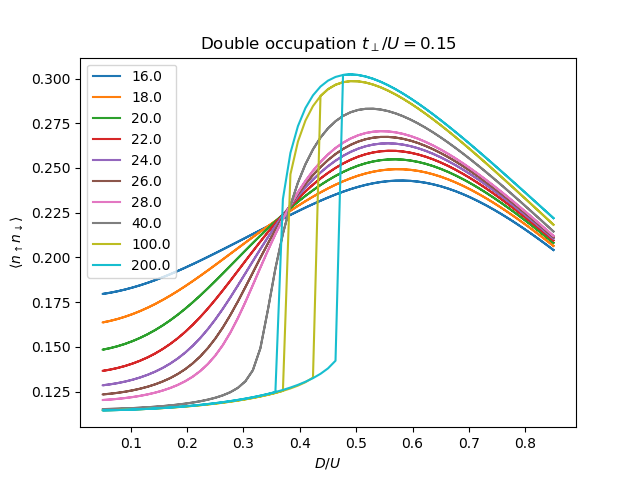
plt.plot(Drange, 2 * epot, '-', label=beta)
plt.title(r'Double occupation $t_\perp/U=0.15$')
plt.ylabel(r'$\langle n_\uparrow n_\downarrow \rangle$')
plt.xlabel(r'$D/U$')
plt.legend()
Out:
[23 20 20 20 20 20 20 19 19 19 19 19 19 18 18 18 18 17 17 17 17 17 17 16 16
16 16 16 16 15 15 15 15 14 14 14 13 13 13 12 12 11 11 11 10 10 9 9 8 8
8 7 7 6 6 6 5 5 5 4 4 1 4 5 5 5 6 6 6 7 7 8 8 8 9
9 10 10 11 11 11 12 12 13 13 14 14 14 14 15 15 15 15 16 16 16 16 16 16 17
17 17 17 17 17 18 18 18 18 19 19 19 19 19 19 20 20 20 20 20 20 20]
[25 20 20 20 20 20 21 21 21 21 20 20 20 20 20 20 20 19 19 19 19 19 19 19 18
18 18 18 18 18 18 17 17 17 17 16 16 15 15 14 14 13 12 12 11 10 10 9 9 8
8 7 7 6 6 6 5 5 5 4 4 1 4 5 5 5 6 6 6 7 7 8 8 9 9
10 10 11 12 12 13 14 14 15 15 16 16 17 17 17 18 18 18 18 18 18 18 18 19 19
19 19 19 19 19 20 20 20 20 20 20 20 21 21 21 21 20 20 20 20 20 21]
[28 23 23 22 21 20 20 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21
21 21 20 20 20 20 20 20 20 19 19 18 17 17 16 15 14 13 12 12 11 10 9 9 8
8 8 7 7 6 6 6 5 5 5 4 1 5 5 5 6 6 6 7 7 8 8 8 9 9
10 11 12 12 13 14 15 16 17 17 18 19 19 20 20 20 20 20 21 21 21 21 21 21 21
21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 20 20 21 22 23 23 24]
[31 25 25 24 23 23 22 21 20 21 21 22 22 22 22 22 22 22 22 22 22 22 22 22 23
23 23 23 23 23 23 23 22 22 22 21 20 19 18 17 16 15 14 13 12 11 10 10 10 9
9 8 8 7 7 6 6 6 5 5 4 1 5 5 6 6 6 7 7 8 8 9 9 10 10
10 11 12 13 14 15 16 17 18 19 20 21 22 22 23 23 23 23 23 23 23 23 23 22 22
22 22 22 22 22 22 22 22 22 22 22 21 21 20 21 22 23 23 24 25 25 25]
[33 28 27 26 25 24 24 23 22 22 20 21 22 22 23 23 23 23 23 24 24 24 24 24 24
24 25 25 25 25 25 25 25 25 24 23 22 21 20 18 17 15 14 13 12 12 12 11 10 10
9 9 8 8 7 7 6 6 5 5 4 1 5 5 6 6 7 7 8 8 9 9 10 10 11
12 12 12 13 14 15 17 18 20 21 22 23 24 25 25 25 25 25 25 25 25 24 24 24 24
24 24 24 23 23 23 23 23 22 22 21 20 22 22 23 24 24 25 26 27 28 29]
[37 31 30 29 28 27 26 24 24 23 23 22 20 21 22 23 23 24 24 24 25 25 25 25 26
26 26 27 27 27 28 28 28 27 26 25 24 23 21 19 17 15 15 15 14 13 13 12 11 10
10 9 8 8 7 7 6 6 5 5 4 1 5 5 6 6 7 7 8 8 9 9 10 11 12
13 13 14 15 15 15 17 19 21 23 24 26 27 27 28 28 28 27 27 27 26 26 26 25 25
25 25 24 24 24 23 23 22 21 20 22 23 23 24 24 26 27 28 29 30 31 32]
[40 32 32 31 30 29 28 27 27 25 24 23 23 22 20 22 23 24 24 25 25 25 26 26 27
27 28 28 29 29 30 30 30 29 29 27 26 24 21 19 17 17 17 16 16 15 13 12 11 10
10 9 8 7 7 6 6 6 5 5 4 1 5 5 5 6 6 7 7 8 9 9 10 11 12
13 14 16 16 17 17 17 19 21 24 26 28 29 30 30 30 30 29 29 28 28 27 27 26 26
25 25 25 24 24 23 22 20 22 23 23 24 25 27 27 28 29 30 31 32 32 34]
[60 49 47 46 45 44 43 41 40 38 37 35 34 33 32 30 29 27 26 25 24 22 21 23 25
27 28 30 31 33 34 36 37 37 37 35 31 31 43 46 34 25 19 16 13 12 10 9 9 8
7 7 6 6 6 5 5 5 4 4 4 1 4 4 5 5 5 6 6 6 7 7 8 9 9
10 12 13 15 19 24 33 46 44 33 31 35 37 38 37 36 34 33 31 30 28 27 25 23 21
22 24 25 26 27 29 30 32 33 34 35 37 38 40 41 43 44 45 46 47 49 51]
[162 134 129 127 124 119 116 114 108 106 103 100 96 93 89 86 84 80
77 73 70 67 64 61 57 55 51 48 44 41 37 33 29 24 19 21
37 12 11 11 10 9 9 8 8 7 7 7 7 6 6 6 5 5
5 5 5 4 4 4 4 1 4 4 4 5 5 5 5 5 6 6
6 7 7 7 7 8 8 9 9 10 10 11 12 13 14 15 19 27
57 37 41 44 48 51 55 57 61 64 68 70 73 77 80 84 86 89
93 96 100 103 106 110 114 116 119 124 127 129 134 137]
[332 276 268 259 258 250 241 236 228 223 215 207 203 197 190 182 177 170
165 158 153 147 141 133 128 121 116 111 103 96 90 83 74 65 56 43
26 18 11 11 10 9 9 8 8 7 7 7 7 6 6 6 5 5
5 5 5 4 4 4 4 1 4 4 4 5 5 5 5 5 6 6
6 7 7 7 7 8 8 9 9 10 10 11 12 13 14 16 18 20
24 31 45 131 111 116 123 128 133 141 148 153 160 165 172 177 182 190
198 203 207 215 223 228 236 241 250 258 263 268 277 282]
Total running time of the script: ( 1 minutes 32.414 seconds)