Study the behavior of the Dimer Bethe lattice in the Transition¶
Specific Regions of the phase diagram are reviewed to inspect the behavior of the insulating state
Out:
[ 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18
18 18 18 18 18 18 18 19 20 21 22 23 25 27 30 33 39 48
68 606 72 66 57 50 54 60 65 66 69 70 72 73 74 75 76 76
77 77 77 78 78 78 78 78 78 77 77 77 76 76 76 75 75 74
74 73 72 72 71 70 70 69 68 68 67 66 65 65 64 63 63 62]
[17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17
17 17 18 18 18 19 20 21 22 23 25 27 29 33 38 45 58 93 96 68 60 58 59 67 72
75 78 80 82 83 84 84 85 85 85 85 85 85 85 84 84 83 82 82 81 80 79 79 78 77
76 75 74 73 73 72 71 70 69 68 67 66 66 65 64]
[ 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16
16 16 16 16 16 16 16 16 16 16 16 16 16 16 17 18 18 19
20 21 22 23 25 27 30 33 37 43 53 73 162 93 75 68 63 62
69 74 77 80 81 83 83 84 84 84 84 83 83 82 81 81 80 79
78 77 77 76 75 74 73 72 71 70 69 68 67 67 66 65 64 63]
[ 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15
15 15 15 15 15 15 15 15 15 15 15 15 15 15 16 16 16 16
17 17 18 18 19 20 21 22 24 26 28 30 33 37 43 51 64 92
373 129 107 95 88 82 77 73 70 67 64 65 66 67 67 67 67 67
67 67 67 66 66 66 65 65 64 64 63 62 62 61 61 60 59 59]
[ 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15
15 15 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14
14 15 15 16 16 17 18 18 19 20 21 22 23 25 26 28 31 34
37 42 49 58 73 101 186 613 238 168 136 116 103 93 85 79 74 70
66 63 60 58 55 53 51 51 51 51 52 52 52 52 51 51 51 51]
[ 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14
14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14
14 14 14 14 14 15 15 16 16 17 17 18 19 20 20 21 23 24
25 27 29 31 34 37 41 46 53 61 72 88 107 127 137 132 120 108
98 89 82 76 71 67 63 60 57 55 53 51 49 47 46 45 43 42]
[13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13
13 13 13 13 13 13 13 13 13 13 13 13 13 14 14 14 14 14 14 14 15 15 16 16 17
17 18 19 19 20 21 22 23 25 26 28 30 32 34 37 40 44 48 53 59 64 70 75 78 79
79 77 74 71 68 65 62 59 56 54 52 50 48 47 45]
[33 31 29 29 29 29 30 30 31 32 32 33 34 36 37 38 40 41 43 44 46 47 49 50 52
53 55 56 58 59 61 62 63 65 66 67 68 69 71 72 73 73 74 75 76 76 77 78 78 78
79 79 79 79 79 79 79 79 79 78 78 78 77 77 76 76 75 75 74 73 73 72 71 71 70
69 69 68 67 66 66 65 64 63 63 62 61 60 60 59]
[31 31 32 32 33 33 34 35 36 38 39 41 42 44 46 47 49 51 53 55 57 59 61 63 65
68 70 72 74 76 78 79 81 83 85 86 88 89 91 92 93 94 95 95 96 97 97 97 97 97
97 97 97 96 96 95 95 94 93 92 92 91 90 89 88 87 86 85 84 82 81 80 79 78 77
76 75 74 73 72 71 70 69 68 67 66 65 64 63 62]
[ 35 36 36 38 39 40 41 43 45 47 49 52 54 57 59 62 65 68
71 74 77 81 84 87 91 94 97 100 103 106 109 112 115 117 119 121
122 123 125 125 126 126 126 126 125 124 124 123 121 120 119 117 116 114
112 111 109 107 106 104 102 100 99 97 95 94 92 90 89 87 86 84
83 81 80 79 77 76 75 74 72 71 70 69 68 67 66 65 64 63]
[ 42 43 45 47 49 52 55 59 62 66 70 75 80 85 91 97 104 111
119 126 134 142 149 156 163 168 172 237 939 149 113 99 92 89 87 88
90 94 100 111 130 178 749 267 197 163 141 126 114 108 106 105 103 102
101 99 98 96 95 93 92 91 89 88 87 85 84 83 82 80 79 78
77 76 74 73 72 71 70 69 68 67 66 65 64 63 62 61 61 60]
[ 58 64 70 98 242 57 45 39 36 34 32 31 30 30 29 28 28 28
27 27 27 27 27 27 27 27 27 27 27 28 28 28 28 29 29 30
30 31 31 32 33 34 35 36 37 38 40 41 43 46 48 51 55 59
65 72 82 95 117 157 275 512 197 142 116 100 89 81 75 70 66 62
60 59 59 59 59 58 58 58 58 57 57 56 56 55 55 54 54 53]
[ 25 24 24 23 23 23 23 22 22 22 22 22 22 22 21 21 21 21
21 21 21 21 21 21 22 22 22 22 22 22 22 23 23 23 23 24
24 24 25 25 26 26 27 27 28 29 30 30 31 32 34 35 36 38
40 42 44 47 50 54 59 65 72 81 93 108 126 141 145 134 119 105
94 85 78 72 67 63 60 57 54 52 50 48 46 45 45 45 45 45]
[20 20 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19
19 19 19 19 20 20 20 20 20 20 21 21 21 21 22 22 22 23 23 24 24 25 25 26 27
27 28 29 30 31 32 33 35 36 38 40 42 44 47 50 53 57 61 66 71 76 80 84 86 85
83 80 76 72 68 64 61 58 56 53 51 49 47 46 44]
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import dmft.dimer as dimer
import dmft.common as gf
import dmft.ipt_imag as ipt
def loop_u_tp(u_int, tp, betarange, seed='mott gap'):
giw_s = []
sigma_iw = []
ekin, epot = [], []
iterations = []
lwn = []
for beta in betarange:
tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=512))
lwn.append(w_n)
giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
if seed == 'mott gap':
giw_d, giw_o = 1 / (1j * w_n + 4j / w_n), np.zeros_like(w_n) + 0j
giw_d, giw_o, loops = dimer.ipt_dmft_loop(
beta, u_int, tp, giw_d, giw_o, tau, w_n)
giw_s.append((giw_d, giw_o))
iterations.append(loops)
g0iw_d, g0iw_o = dimer.self_consistency(
1j * w_n, 1j * giw_d.imag, giw_o.real, 0., tp, 0.25)
siw_d, siw_o = ipt.dimer_sigma(u_int, tp, g0iw_d, g0iw_o, tau, w_n)
sigma_iw.append((siw_d.copy(), siw_o.copy()))
ekin.append(dimer.ekin(giw_d, giw_o, w_n, tp, beta))
epot.append(dimer.epot(giw_d, w_n, beta,
u_int ** 2 / 4 + tp**2, ekin[-1], u_int))
print(np.array(iterations))
# last division in energies because I want per spin epot
return np.array(giw_s), np.array(sigma_iw), np.array(ekin) / 4, np.array(epot) / 4, w_n
urange = np.arange(2.8, 3.4, .1)
data = []
temp = np.linspace(0.015, 0.06, 90)
betarange = 1 / temp
for u_int in urange:
giw_s, sigma_iw, ekin, epot, w_n = loop_u_tp(
u_int, .3, betarange, 'mott gap')
data.append((giw_s, sigma_iw, ekin, epot, w_n, u_int))
for u_int in urange:
giw_s, sigma_iw, ekin, epot, w_n = loop_u_tp(
u_int, .3, betarange, 'met')
data.append((giw_s, sigma_iw, ekin, epot, w_n, u_int))
for sim in data:
giw_s, sigma_iw, ekin, epot, w_n, u_int = sim
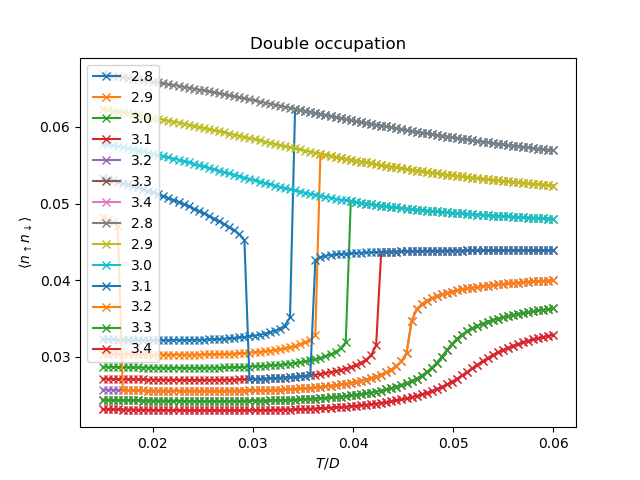
plt.plot(1 / betarange, 2 * epot / u_int, 'x-', label=u_int)
plt.title(r'Double occupation')
plt.ylabel(r'$\langle n_\uparrow n_\downarrow \rangle$')
plt.xlabel(r'$T/D$')
plt.legend()
plt.show()
Total running time of the script: ( 2 minutes 14.274 seconds)