Scattering rates change in Temperature¶
Explore the low energy expansion of the Matsubara self-energy. The zero frequency value being the scattering rate. Figure is discussed in reference [Najera2017]
| [Najera2017] | O. Nájera, Civelli, M., V. Dobrosavljevic, & Rozenberg, M. J. (2017). Resolving the VO_2 controversy: Mott mechanism dominates the insulator-to-metal transition. Physical Review B, 95(3), 035113. http://dx.doi.org/10.1103/physrevb.95.035113 |
# Created Mon Mar 7 01:14:02 2016
# Author: Óscar Nájera
from __future__ import division, absolute_import, print_function
from math import log, ceil
import numpy as np
import matplotlib.pyplot as plt
import dmft.dimer as dimer
import dmft.common as gf
import dmft.ipt_imag as ipt
def loop_beta(u_int, tp, betarange, seed='ins'):
"""Solves IPT dimer and return Im Sigma_AA, Re Simga_AB
returns list len(betarange) x 2 Sigma arrays """
sigma_iw = []
iterations = []
for beta in betarange:
tau, w_n = gf.tau_wn_setup(
dict(BETA=beta, N_MATSUBARA=max(2**ceil(log(4 * beta) / log(2)), 256)))
giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
if seed == 'ins':
giw_d, giw_o = 1 / (1j * w_n - 4j / w_n), np.zeros_like(w_n) + 0j
giw_d, giw_o, loops = dimer.ipt_dmft_loop(
beta, u_int, tp, giw_d, giw_o, tau, w_n, 1e-3)
iterations.append(loops)
g0iw_d, g0iw_o = dimer.self_consistency(
1j * w_n, 1j * giw_d.imag, giw_o.real, 0., tp, 0.25)
siw_d, siw_o = ipt.dimer_sigma(u_int, tp, g0iw_d, g0iw_o, tau, w_n)
sigma_iw.append((siw_d.imag, siw_o.real))
print(np.array(iterations))
return sigma_iw
Calculate the dimer solution for Metals up to Uc2 in the in the given temperature range. Include the behavior of 2 insulators inside the coexistence region.
temp = np.arange(1 / 500., .05, .001)
BETARANGE = 1 / temp
U_intm = np.linspace(0, 3, 13)
sigmasM_U = [loop_beta(u_int, .3, BETARANGE, 'met') for u_int in U_intm]
U_inti = [2.5, 3.]
sigmasI_U = [loop_beta(u_int, .3, BETARANGE, 'ins') for u_int in U_inti]
Out:
[487 327 245 198 162 142 126 111 100 90 85 75 70 65 64 59 59 54
49 49 49 44 44 44 39 39 38 34 34 34 33 33 29 29 29 28
28 28 28 28 24 24 23 23 23 23 23 23]
[481 322 239 193 162 136 121 106 100 90 80 75 70 64 64 59 54 54
49 49 44 44 44 39 39 39 38 34 34 33 33 33 29 29 28 28
28 28 28 24 24 23 23 23 23 23 23 23]
[464 310 233 187 156 131 115 105 95 85 79 74 69 64 59 54 54 49
49 44 44 43 39 39 38 34 34 33 33 33 29 29 28 28 28 28
24 24 23 23 23 23 23 23 23 23 19 19]
[435 287 216 175 145 125 109 99 89 79 74 69 64 59 54 49 48 44
43 43 38 38 38 33 33 33 33 29 28 28 28 28 28 24 23 23
23 23 23 23 23 19 19 19 19 19 18 18]
[405 269 199 158 133 113 98 88 78 73 68 63 58 53 48 48 43 43
38 38 38 33 33 33 32 28 28 28 28 24 23 23 23 23 23 23
19 19 19 19 18 18 18 18 18 18 18 17]
[364 245 180 146 121 101 87 77 72 62 57 52 52 47 42 42 37 37
33 33 32 28 28 28 27 27 23 23 23 23 23 19 19 18 18 18
18 18 18 18 17 14 14 14 14 14 14 14]
[331 219 162 128 104 89 79 70 60 56 51 46 42 41 37 36 32 32
31 27 27 27 23 23 23 22 22 19 18 18 18 18 18 18 17 14
14 14 14 14 14 14 14 13 13 13 10 10]
[296 193 142 110 91 77 68 58 54 49 45 40 36 35 31 31 27 26
26 22 22 22 22 18 18 18 18 17 14 14 14 14 14 14 14 13
13 12 11 10 10 10 10 10 10 10 10 9]
[265 171 127 96 82 69 60 51 47 42 38 34 30 29 25 25 25 21
21 21 17 17 17 17 16 13 13 13 13 13 12 11 10 10 10 10
9 9 9 10 10 11 11 12 12 12 12 13]
[236 148 110 85 69 57 48 44 40 36 32 28 24 24 23 20 20 17
16 16 13 13 13 13 12 10 10 9 9 9 10 11 11 12 12 13
13 14 14 14 15 15 15 15 16 16 16 16]
[205 128 94 71 56 48 40 36 30 26 25 22 19 18 18 15 15 12
12 12 11 9 10 11 11 12 12 13 14 14 15 16 16 17 17 18
18 18 19 19 19 19 20 20 20 20 20 20]
[175 107 73 56 46 36 30 26 23 20 17 16 14 13 12 12 12 12
12 13 13 14 15 15 16 17 18 19 20 21 22 23 23 24 25 25
26 26 26 27 27 27 27 27 27 27 26 26]
[138 80 54 42 33 27 22 19 16 14 12 12 13 13 14 15 15 16
18 19 21 22 24 26 29 31 33 35 37 39 41 42 43 43 44 44
43 43 42 41 40 39 38 37 36 35 34 33]
[ 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 10 10 10 10 11 12 13 18 47 28
23 21 16 15 15 18 16 15 18 12 20 20 19 18 21 20 21 21 21 21 17 17 21]
[ 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7
7 8 8 8 8 9 9 10 11 12 14 17 27 55 39 32 29 27 25 23 22 21 20]
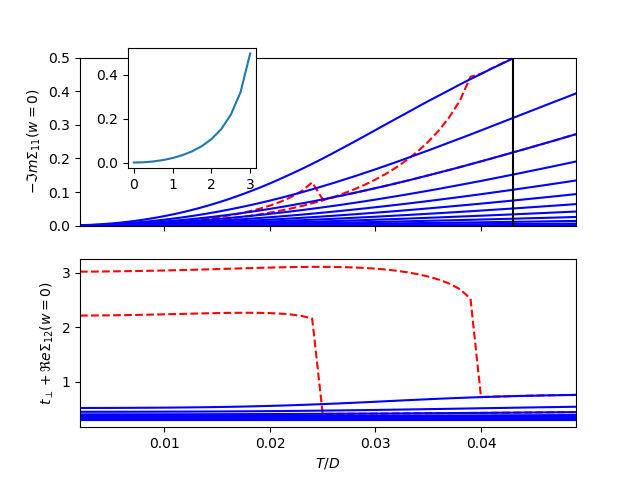
Plot the zero frequency extrapolation of the self-energy. Top panel shows for all metals how upon cooling they become more coherent. Interestingly enough is the insulators is red showning even higher coherence(lower value of the scattering rate) than the metal. This is how the dimer Mott insulator fundamentally differs from the Single Site DMFT Mott insulator. When performing a correct analytical continuation of the Self-energy on the insulator it becomes evident that it is gaped at zero frequency.
The lower panel shows the effective hybridization of the dimers. It is barely changed in the metal but is strongly boosted in the insulator.
def plot_zero_w(function_array, iter_range, tp, betarange, ax, color):
"""Plot the zero frequency extrapolation of a function
Parameters
----------
function_array: real ndarray
contains the function (G, Sigma) to linearly fit over 2 first frequencies
iter_range: list floats
values of changing variable U or tp
berarange: real ndarray 1D, values of beta
entry: 0, 1 corresponds to diagonal or off-diagonal entry of function
label_head: string for label
ax, dx: matplotlib axis to plot in
"""
sig_11_0 = []
rtp = []
for j, u in enumerate(iter_range):
sig_11_0.append([])
rtp.append([])
for i, beta in list(enumerate(betarange)):
tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=2))
sig_11_0[j].append(np.polyfit(
w_n, function_array[j][i][0][:2], 1)[1])
rtp[j].append(np.polyfit(w_n, function_array[j][i][1][:2], 1)[1])
ax[0].plot(1 / BETARANGE, -np.array(sig_11_0[j]), color, label=str(u))
ax[1].plot(1 / BETARANGE, tp + np.array(rtp[j]), color, label=str(u))
ax[0].set_ylabel(r'$-\Im m \Sigma_{11}(w=0)$')
ax[1].set_ylabel(r'$t_\perp + \Re e\Sigma_{12}(w=0)$')
ax[1].set_xlabel('$T/D$')
ax[1].set_xlim([min(temp), max(temp)])
return np.array(sig_11_0)
fig, si = plt.subplots(2, 1, sharex=True)
sig_11_0i = plot_zero_w(sigmasI_U, U_inti, .3, BETARANGE, si, 'r--')
# fig, si = plt.subplots(2, 1, sharex=True)
sig_11_0m = plot_zero_w(sigmasM_U, U_intm, .3, BETARANGE, si, 'b')
si[0].set_ylim([0, 0.5])
ax = fig.add_axes([.2, .65, .2, .25])
ax.plot(U_intm, -sig_11_0m[:, -7])
ax.set_xticks(np.arange(0, 3.1, 1))
si[0].axvline(temp[-7], color='k')
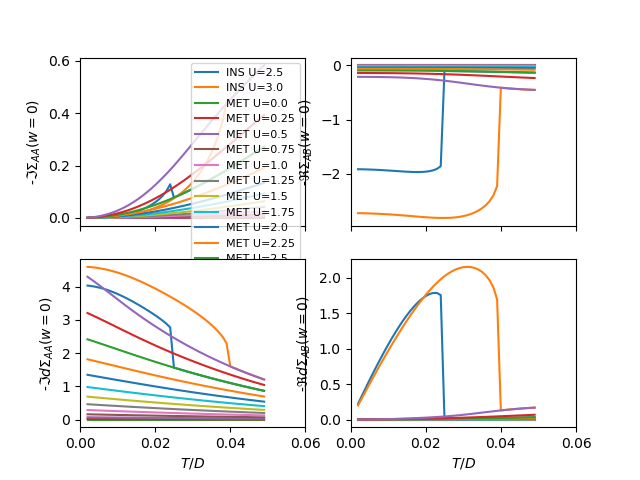
Plot the derivative at zero frequency of the self-energy
def plot_der_zero_w(function_array, iter_range, betarange, entry, label_head, ax, dx):
"""Plot the zero frequency extrapolation of a function
Parameters
----------
function_array: real ndarray
contains the function (G, Sigma) to linearly fit over 2 first frequencies
iter_range: list floats
values of changing variable U or tp
berarange: real ndarray 1D, values of beta
entry: 0, 1 corresponds to diagonal or off-diagonal entry of function
label_head: string for label
ax, dx: matplotlib axis to plot in
"""
for j, u in enumerate(iter_range):
dat = []
for i, beta in list(enumerate(betarange)):
tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=20))
dat.append(np.polyfit(
w_n[:2], function_array[j][i][entry][:2], 1))
ax.plot(1 / BETARANGE, -np.array(dat)
[:, 1], label=label_head + str(u))
dx.plot(1 / BETARANGE, -np.array(dat)
[:, 0], label=label_head + str(u))
f, (si, ds) = plt.subplots(2, 2, sharex=True)
plot_der_zero_w(sigmasI_U, U_inti, BETARANGE, 0, 'INS U=', si[0], ds[0])
plot_der_zero_w(sigmasM_U, U_intm, BETARANGE, 0, 'MET U=', si[0], ds[0])
plot_der_zero_w(sigmasI_U, U_inti, BETARANGE, 1, 'INS U=', si[1], ds[1])
plot_der_zero_w(sigmasM_U, U_intm, BETARANGE, 1, 'MET U=', si[1], ds[1])
si[0].legend(loc=0, prop={'size': 8})
si[0].set_ylabel(r'-$\Im \Sigma_{AA}(w=0)$')
ds[0].set_ylabel(r'-$\Im d\Sigma_{AA}(w=0)$')
si[1].set_ylabel(r'-$\Re \Sigma_{AB}(w=0)$')
ds[1].set_ylabel(r'-$\Re d\Sigma_{AB}(w=0)$')
ds[0].set_xlim([0, .06])
ds[0].set_xlabel('$T/D$')
ds[1].set_xlabel('$T/D$')
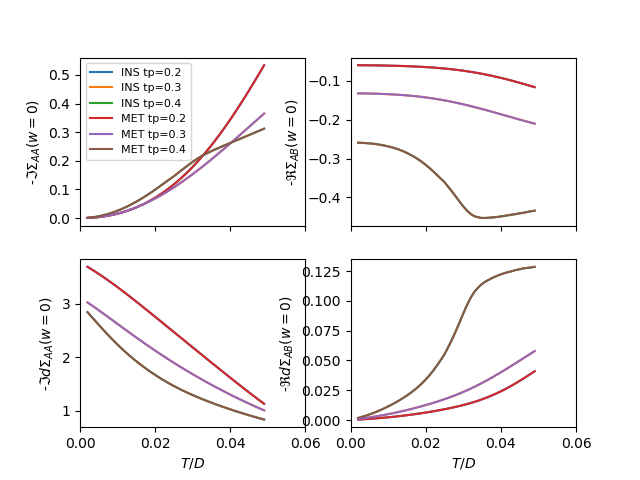
Changing tp in the METAL dome for metal and insulator Fix U
tp_r = [0.2, 0.3, 0.4]
sigmasM_tp = [loop_beta(2.7, tp, BETARANGE, 'M') for tp in tp_r]
sigmasI_tp = [loop_beta(2.7, tp, BETARANGE, 'I') for tp in tp_r]
f, (si, ds) = plt.subplots(2, 2, sharex=True)
plot_der_zero_w(sigmasI_tp, tp_r, BETARANGE, 0, 'INS tp=', si[0], ds[0])
plot_der_zero_w(sigmasM_tp, tp_r, BETARANGE, 0, 'MET tp=', si[0], ds[0])
plot_der_zero_w(sigmasI_tp, tp_r, BETARANGE, 1, 'INS tp=', si[1], ds[1])
plot_der_zero_w(sigmasM_tp, tp_r, BETARANGE, 1, 'MET tp=', si[1], ds[1])
si[0].set_ylabel(r'-$\Im \Sigma_{AA}(w=0)$')
ds[0].set_ylabel(r'-$\Im d\Sigma_{AA}(w=0)$')
si[1].set_ylabel(r'-$\Re \Sigma_{AB}(w=0)$')
ds[1].set_ylabel(r'-$\Re d\Sigma_{AB}(w=0)$')
ds[0].set_xlim([0, .06])
si[0].legend(loc=0, prop={'size': 8})
ds[0].set_xlabel('$T/D$')
ds[1].set_xlabel('$T/D$')
Out:
[129 82 64 46 40 34 29 28 23 18 18 18 14 14 13 12 13 15
16 17 17 18 18 18 19 19 19 19 19 19 19 19 19 18 18 18
18 18 18 17 17 17 17 16 16 16 16 16]
[183 110 79 58 47 40 33 27 24 23 20 17 16 14 13 12 12 11
11 12 12 13 14 14 15 16 17 18 19 19 20 21 22 22 23 23
24 24 24 25 25 25 25 25 25 25 25 25]
[157 96 64 47 38 30 24 20 17 14 12 10 9 9 9 10 10 10
10 10 10 9 9 9 13 16 19 22 25 27 28 28 26 25 23 21
20 19 18 17 16 15 15 14 14 13 12 12]
[129 82 64 46 40 34 29 28 23 18 18 18 14 14 13 12 13 15
16 17 17 18 18 18 19 19 19 19 19 19 19 19 19 18 18 18
18 18 18 17 17 17 17 16 16 16 16 16]
[183 110 79 58 47 40 33 27 24 23 20 17 16 14 13 12 12 11
11 12 12 13 14 14 15 16 17 18 19 19 20 21 22 22 23 23
24 24 24 25 25 25 25 25 25 25 25 25]
[157 96 64 47 38 30 24 20 17 14 12 10 9 9 9 10 10 10
10 10 10 9 9 9 13 16 19 22 25 27 28 28 26 25 23 21
20 19 18 17 16 15 15 14 14 13 12 12]
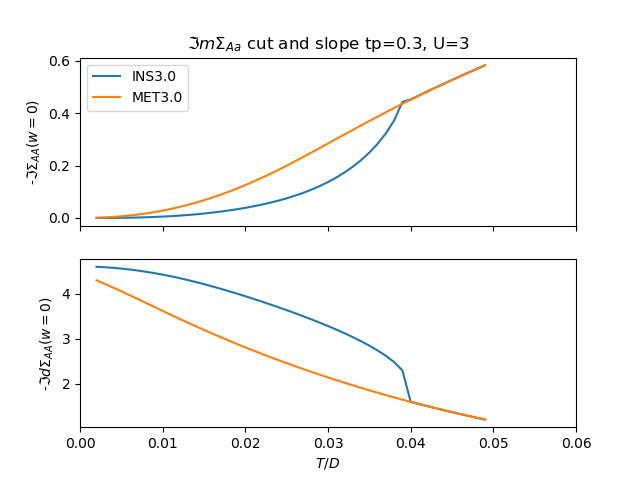
Fine graphics
f, (si, ds) = plt.subplots(2, 1, sharex=True)
plot_der_zero_w([sigmasI_U[1]], [3.], BETARANGE, 0, 'INS', si, ds)
plot_der_zero_w([sigmasM_U[-1]], [3.], BETARANGE, 0, 'MET', si, ds)
si.set_title(r'$\Im m\Sigma_{Aa}$ cut and slope tp=0.3, U=3')
si.set_ylabel(r'-$\Im \Sigma_{AA}(w=0)$')
ds.set_ylabel(r'-$\Im d\Sigma_{AA}(w=0)$')
ds.set_xlim([0, .06])
si.legend(loc=0, prop={'size': 10})
ds.set_xlabel('$T/D$')
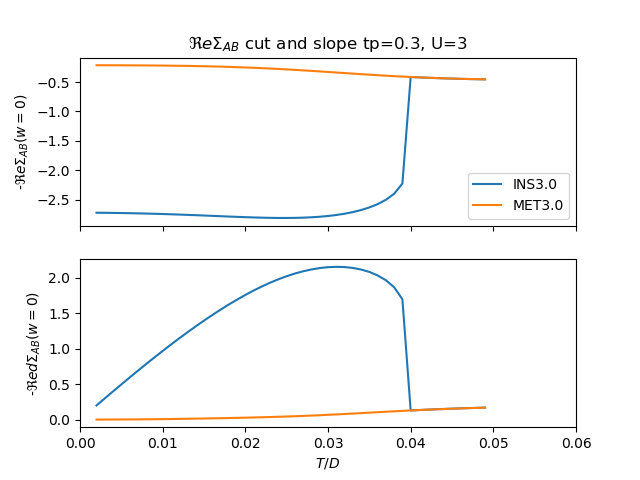
f, (si, ds) = plt.subplots(2, 1, sharex=True)
plot_der_zero_w([sigmasI_U[1]], [3.], BETARANGE, 1, 'INS', si, ds)
plot_der_zero_w([sigmasM_U[-1]], [3.], BETARANGE, 1, 'MET', si, ds)
si.set_title(r'$\Re e\Sigma_{AB}$ cut and slope tp=0.3, U=3')
si.set_ylabel(r'-$\Re e \Sigma_{AB}(w=0)$')
ds.set_ylabel(r'-$\Re e d\Sigma_{AB}(w=0)$')
ds.set_xlim([0, .06])
si.legend(loc=0, prop={'size': 10})
ds.set_xlabel('$T/D$')
Total running time of the script: ( 1 minutes 30.980 seconds)