Dimer Mott transition Optical response with temperature

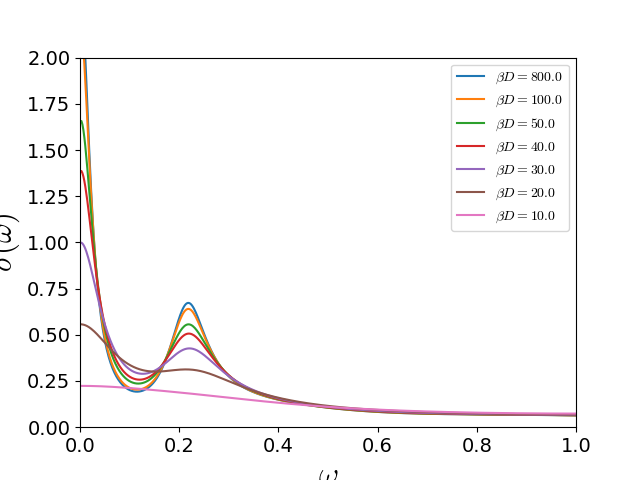
Track the optical conductivity of the correlated metal as the system is warmed up. Temperature induces a loss of spectral weight and coherence in the quasiparticles. Is is clear that the Drude peak and the Mid-Infra-Red resonance broaden. The high energy features remain broad. For reference in IPT at 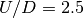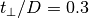the insulator to metal transition occurs around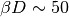

See also

Dimer Mott transition The insulator transition order parameter

# author: Óscar Nájera

from __future__ import division, absolute_import, print_function

import numpy as np
import matplotlib.pyplot as plt

import dmft.common as gf
import dmft.ipt_real as ipt
import dmft.dimer as dimer

plt.matplotlib.rcParams.update({'axes.labelsize': 22,
                                'xtick.labelsize': 14, 'ytick.labelsize': 14,
                                'axes.titlesize': 22,
                                'mathtext.fontset': 'cm'})

w = np.linspace(-4, 4, 2**12)
dw = w[1] - w[0]


U = 2.5
tp = 0.3
gss = gf.semi_circle_hiltrans(w + 5e-3j - tp)
gsa = gf.semi_circle_hiltrans(w + 5e-3j + tp)
eps_k = np.linspace(-1, 1, 61)
pos_freq = w > 0
nuv = w[pos_freq]

BETARANGE = [800., 100., 50., 40., 30., 20., 10.]
plt.close('all')
for BETA in BETARANGE:
    nfp = gf.fermi_dist(w, BETA)
    (gss, gsa), (ss, sa) = ipt.dimer_dmft(
        U, tp, nfp, w, dw, gss, gsa, conv=1e-4)

    s_intra, s_inter = dimer.optical_conductivity(BETA, ss, sa, w, tp, eps_k)

    ddm_sigma_E_sum = .5 * (s_intra + s_inter)

    plt.plot(nuv, ddm_sigma_E_sum, label=r'$\beta D={}$'.format(BETA))

plt.xlabel(r'$\omega$')
plt.ylabel(r'$\sigma(\omega)$')
plt.xlim(0, 1)
plt.ylim(0, 2)
plt.legend(loc=0)

Total running time of the script: ( 0 minutes 3.336 seconds)