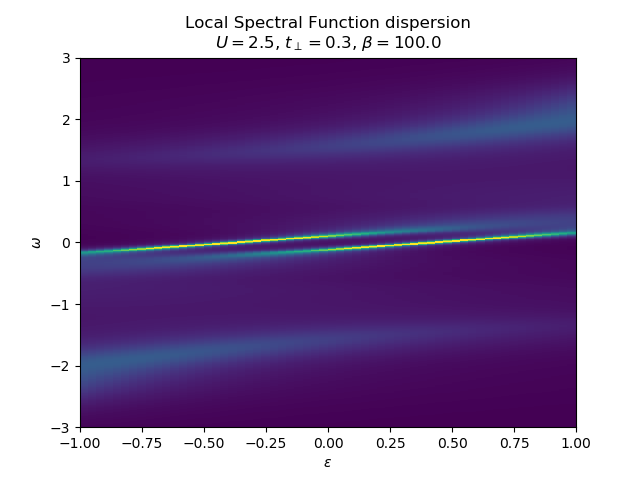
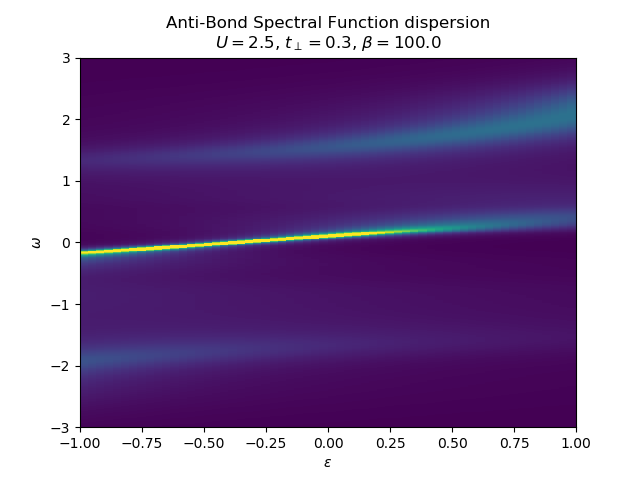
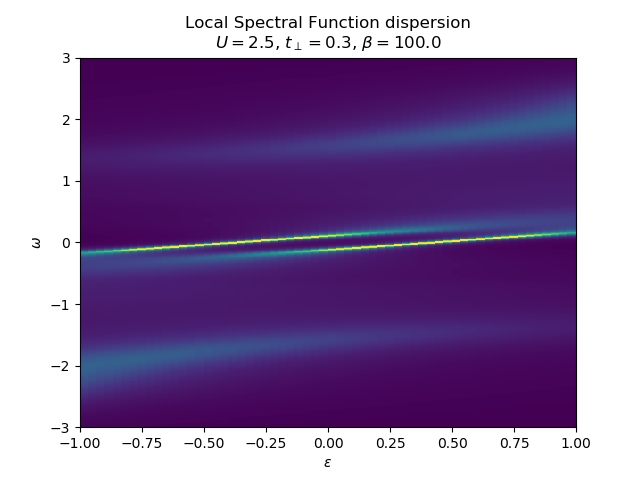
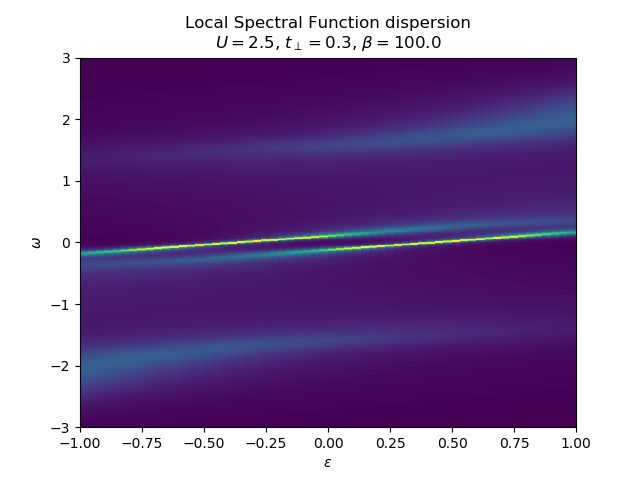
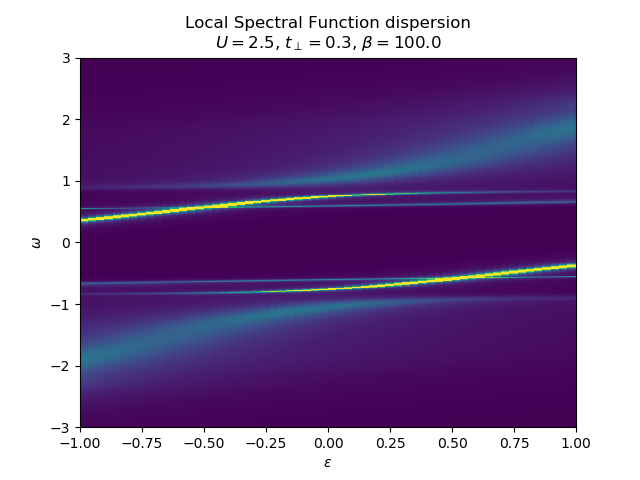
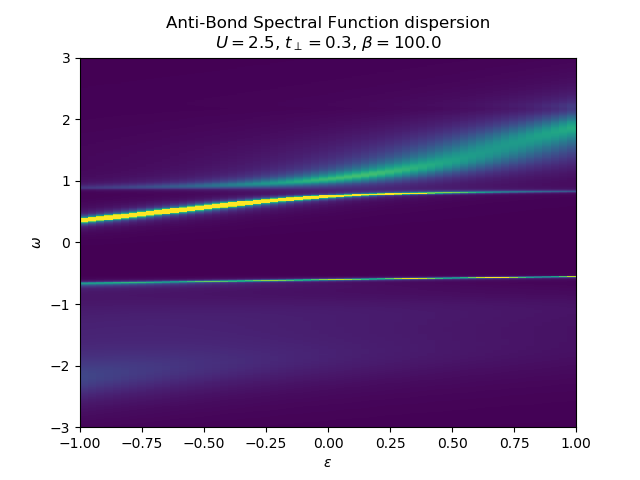
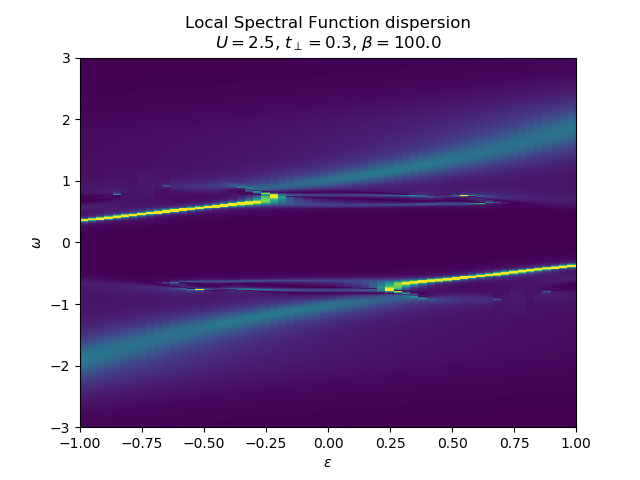
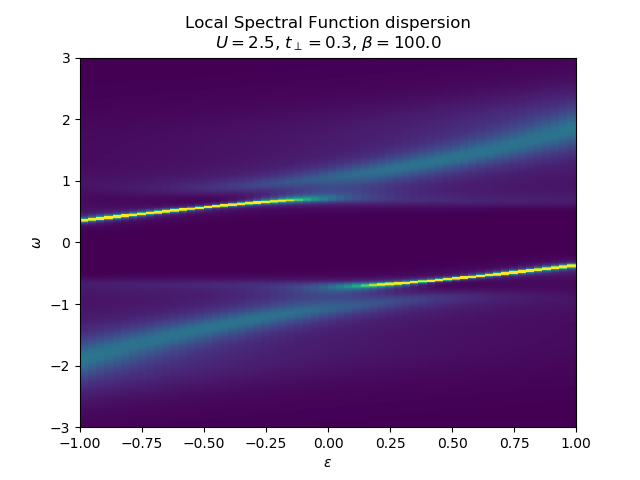
Various schemes for obtaining the spectral dispersion

• 
• 
• 
• 
• 
• 
• 
• 

# Created Mon Apr 11 14:17:29 2016
# Author: Óscar Nájera

from __future__ import division, absolute_import, print_function

import matplotlib.pyplot as plt
import numpy as np

import dmft.common as gf
import dmft.dimer as dimer
import dmft.ipt_imag as ipt
from dmft.plot import plot_band_dispersion


def ipt_u_tp(u_int, tp, beta, seed='ins'):
    tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=1024))
    giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
    if seed == 'ins':
        giw_d, giw_o = 1 / (1j * w_n + 4j / w_n), np.zeros_like(w_n) + 0j

    giw_d, giw_o, loops = dimer.ipt_dmft_loop(
        beta, u_int, tp, giw_d, giw_o, tau, w_n, 1e-12)
    g0iw_d, g0iw_o = dimer.self_consistency(
        1j * w_n, 1j * giw_d.imag, giw_o.real, 0., tp, 0.25)
    siw_d, siw_o = ipt.dimer_sigma(u_int, tp, g0iw_d, g0iw_o, tau, w_n)

    return siw_d, siw_o, w_n


def construct_dispersions(BETA, u_int, tp, seed):
    siw_d, siw_o, w_n = ipt_u_tp(u_int, tp, BETA, seed)

    w = np.linspace(-3, 3, 800)
    eps_k = np.linspace(-1., 1., 61)
    w_set = np.arange(200)

    ss = gf.pade_continuation(
        1j * siw_d.imag + siw_o.real, w_n, w, w_set)  # A-bond
    sa = gf.pade_continuation(
        1j * siw_d.imag - siw_o.real, w_n, w, w_set)  # bond
    lat_gfs = 1 / np.add.outer(-eps_k, w - tp + 5e-2j - ss)
    lat_gfa = 1 / np.add.outer(-eps_k, w + tp + 5e-2j - sa)
    Aw = np.clip(-.5 * (lat_gfa + lat_gfs).imag / np.pi, 0, 2)

    title = 'Spectral Function dispersion\n$U={}$, $t_\\perp={}$, $\\beta={}$'.format(
        u_int, tp, BETA)

    # Continuate in Sigma Diagonal then return to local
    plot_band_dispersion(w, Aw, 'Local ' + title, eps_k, 'intensity')
    file_r = "Aew_B{}U{}tp{}_{}_".format(BETA, u_int, tp, seed)
    plt.savefig(file_r + 'psl.png', format='png',
                transparent=False, bbox_inches='tight', pad_inches=0.05)

    # Continuate in Sigma Diagonal only plot anti-bonding
    Aw = np.clip(-lat_gfs.imag / np.pi, 0, 2)
    plot_band_dispersion(w,  Aw, 'Anti-Bond ' + title, eps_k,  'intensity')
    plt.savefig(file_r + 'psa.png', format='png',
                transparent=False, bbox_inches='tight', pad_inches=0.05)

    # Continuate the dispersion on G(e, w)_AA
    Ag = []
    for e in eps_k:
        gd = dimer.mat_inv(1j * w_n - e - 1j * siw_d.imag, -tp - siw_o.real)[0]
        Ag.append(np.clip(
            np.abs(-gf.pade_continuation(gd, w_n, w + 1e-2j, w_set).imag / np.pi), 0, 2))

    plot_band_dispersion(w, np.asarray(
        Ag), 'Local ' + title, eps_k, 'intensity')
    plt.savefig(file_r + 'pgl.png', format='png',
                transparent=False, bbox_inches='tight', pad_inches=0.05)

    # Continuate on G(e, w)_AA but skipping frequencies for smooth output
    w_set = np.arange(0, 200, 4)
    Ag = []
    for e in eps_k:
        gd = dimer.mat_inv(1j * w_n - e - 1j * siw_d.imag, -tp - siw_o.real)[0]
        Ag.append(np.clip(
            np.abs(-gf.pade_continuation(gd, w_n, w + 1e-2j, w_set).imag / np.pi), 0, 2))

    plot_band_dispersion(w, np.asarray(
        Ag), 'Local ' + title, eps_k, 'intensity')
    plt.savefig(file_r + 'pgls.png', format='png',
                transparent=False, bbox_inches='tight', pad_inches=0.05)


construct_dispersions(100., 2.5, .3, 'met')
construct_dispersions(100., 2.5, .3, 'ins')

Total running time of the script: ( 0 minutes 7.588 seconds)