Form of the Greens Functions

# Author: Óscar Nájera

from __future__ import (absolute_import, division, print_function,
                        unicode_literals)

from math import log, ceil
import matplotlib.pyplot as plt
import numpy as np

import dmft.common as gf
import dmft.ipt_imag as ipt
import dmft.dimer as dimer


def ipt_u_tp(u_int, tp, beta, seed='ins'):
    tau, w_n = gf.tau_wn_setup(dict(BETA=beta, N_MATSUBARA=2**8))
    tau, w_n = gf.tau_wn_setup(
        dict(BETA=beta, N_MATSUBARA=max(2**ceil(log(8 * beta) / log(2)), 256)))
    giw_d, giw_o = dimer.gf_met(w_n, 0., 0., 0.5, 0.)
    if seed == 'ins':
        giw_d, giw_o = 1 / (1j * w_n + 4j / w_n), np.zeros_like(w_n) + 0j

    giw_d, giw_o, loops = dimer.ipt_dmft_loop(
        beta, u_int, tp, giw_d, giw_o, tau, w_n, 1e-7)
    g0iw_d, g0iw_o = dimer.self_consistency(
        1j * w_n, 1j * giw_d.imag, giw_o.real, 0., tp, 0.25)
    siw_d, siw_o = ipt.dimer_sigma(u_int, tp, g0iw_d, g0iw_o, tau, w_n)

    return giw_d, giw_o, siw_d, siw_o, g0iw_d, g0iw_o, w_n

Insulator

u_int = 3.5
BETA = 85.94
tp = 0.3
title = r'IPT lattice dimer $U={}$, $t_\perp={}$, $\beta={}$'.format(
    u_int, tp, BETA)
giw_d, giw_o, siw_d, siw_o, g0iw_d, g0iw_o, w_n = ipt_u_tp(
    u_int, tp, BETA, 'met')

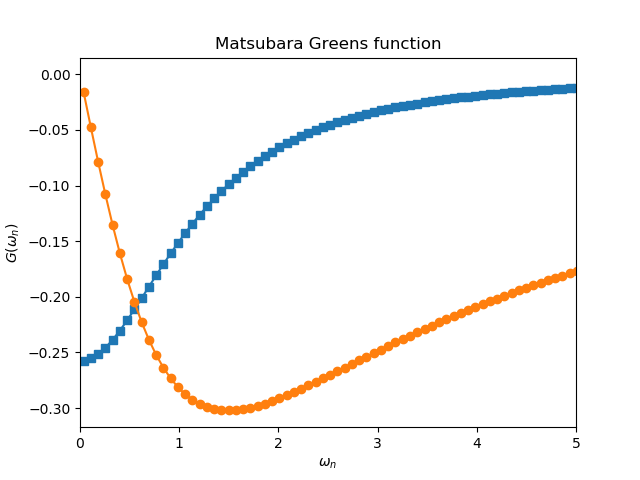
plt.figure('G')
plt.plot(w_n, giw_o.real, 's-')
plt.plot(w_n, giw_d.imag, 'o-')
plt.title("Matsubara Greens function")
plt.xlabel(r'$\omega_n$')
plt.ylabel(r'$G(\omega_n)$')
plt.xlim([0, 5])

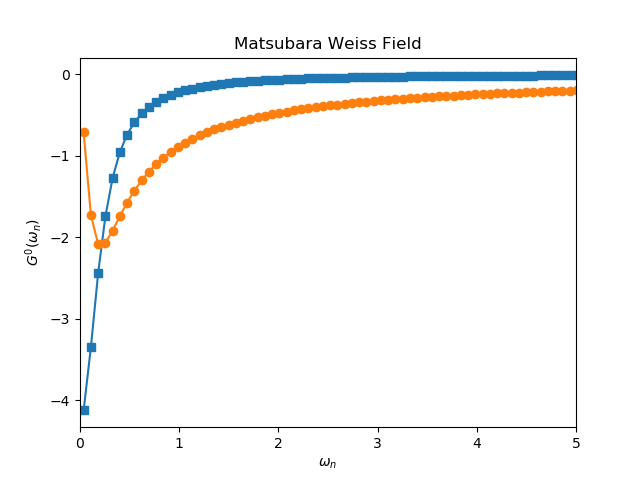
plt.figure('G0')
plt.plot(w_n, g0iw_o.real, 's-')
plt.plot(w_n, g0iw_d.imag, 'o-')
plt.title("Matsubara Weiss Field")
plt.xlabel(r'$\omega_n$')
plt.ylabel(r'$G^0(\omega_n)$')
plt.xlim([0, 5])
plt.show()

• 
• 

Total running time of the script: ( 0 minutes 0.212 seconds)